1/1/21 和分法とスターリング数 Mathlog 和分法とスターリング数 magolors magolors フォローする 解説 大学数学以上スターリングの公式はガンマ関数の漸近展開から導出される。 この節ではガンマ関数の基本的な性質について復習するが、すでによく知っている人は次の節まで読み飛ばしてよい。 α > 0 とするとき、ガンマ関数は次の積分で定義される: (1) (1) Γ ( α) = ∫の近似値を与える公式で, と表わされる。これは,n を非常に大きいとしての近似式で,n→∞ のとき両辺の比が1に近づくことを意味するが,n が小さいときでも,近似の精度は比較
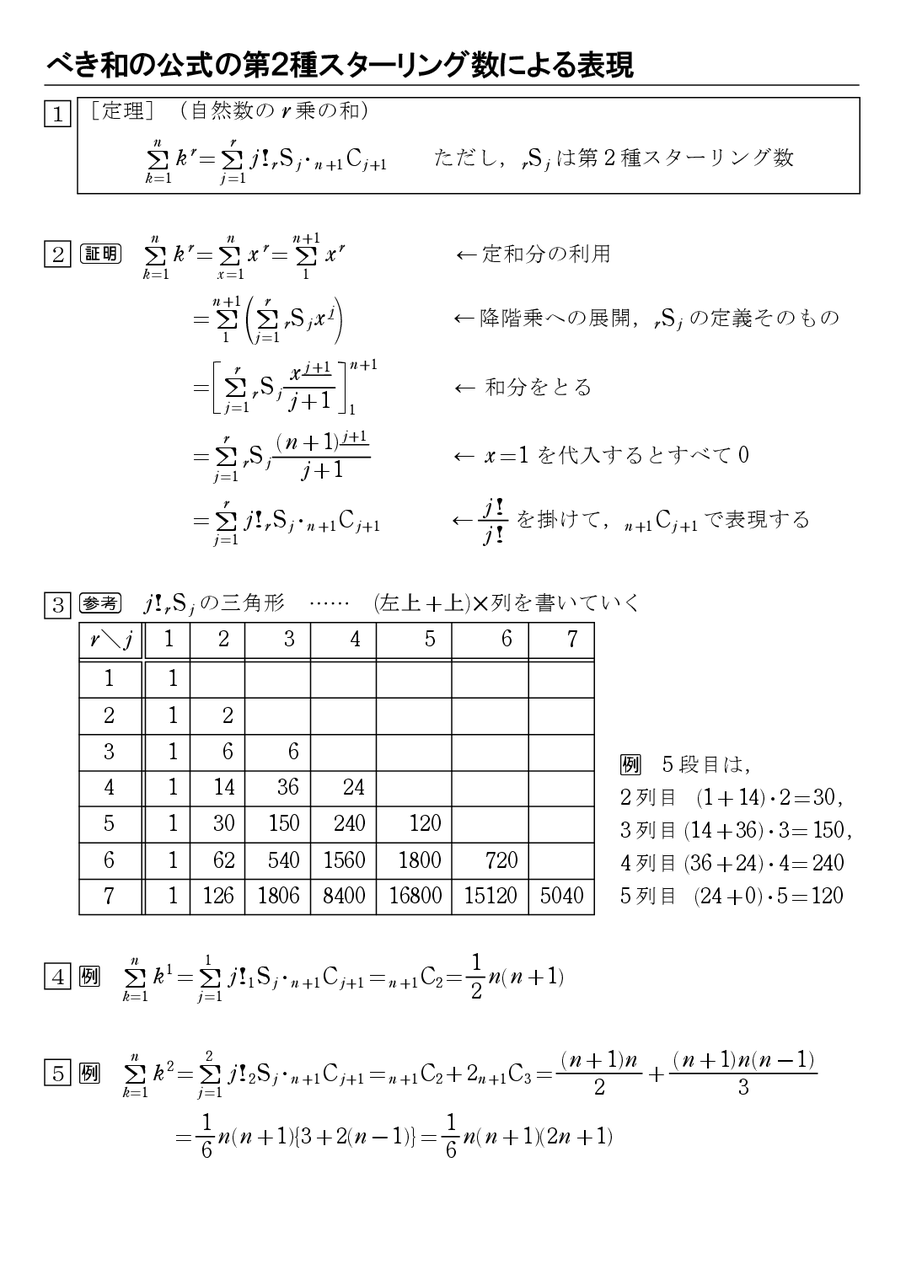
べき和の公式の第2種スターリング数による表現 怜悧玲瓏 高校数学を天空から俯瞰する
スターリング 数学
スターリング 数学-スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (英語版) が1730年に彼の著書 Methodus Differentialis で導入した数 1 である。第1種スターリング数 第1種スターリング数(表) 第2種スターリング数 第2種スターリング数(表)




第2種スターリング数の性質 数学a フリー教材開発コミュニティ Ftext
3/5/08 まずは普通のスターリングの公式 統計力学では良く階乗の計算が出てくる それが『アボガドロ数程度の大きさの整数』の階乗だったりするものだから, 定義に従って具体的な値を算出するのは不可能であるし, もう桁が幾つか違っていてもどうでもいいやと思えるほどに大き過ぎる値となるスターリングの公式による階乗・順列・組み合わせの近似計算 スターリングの公式で近似計算します。指数部を分けて計算・表示するので、大きい値でもオーバーフローしません。 値を入力してエンターを押してください。 階乗 n!!10/5/17 Stirling の公式 lim n → ∞ n!
1/2/18 数え上げに関する話題として分割数や スターリン グ数は時折登場しますが、どちらも 写像 12相と呼ばれる広い枠組みに含まれています。 前回は分割数を、今回は スターリン グ数を勉強しました。 なお、 スターリン グ数 (の考え方) が使える問題として以下があります (他にもあったら大募集なのん) yukicoder No391 CODING WAR yukicoder No140 みん2 π n ( n / e) n = 1 は n が 十分に大きいとき, n!スターリング数 スターリング数 \(\newcommand{\stirlingI}{\genfrac{0pt}{}} % 第1種スターリング数\newcommand{\stirlingII}{\genfrac\{\}{0pt}{}} % 第2種スターリング数\newcommand{\risingFactorial}2{{#1}^{\overline{#2}}}\newcommand{\fallingFactorial}2{{#1}^{\underline{#2}}}\)次のような記号を導入する: \begin{align*} \risingFactorial{x}{n}&=x(x1)\dotsb(xn1), \\
スターリングの公式 結論から言うと、スターリングの公式は次のように表されます。 $$ n !第 種スターリング数を求めるプログラム 自然数 に対してリスト を作る リスト同士の掛け算 第 種スターリング数 を求めるプログラム ただし、このプログラミングだと逆に表示されてしまうので、質問するときは例えば、 と質問すること。 この式をスターリングの近似式と言いまして、統計力学で重要な式になります。 Lagrangeの未定係数法 そしてもう1つのテクニックは、Lagrangeの未定係数法です。 これはある条件に従う点の中で極値を与える変数を求めるテクニックになります。




Amazon Co Jp 925スターリングシルバー媒体サテン数2チャームとペンダント Clothing Accessories




第2種スターリング数 高校生向け 2 怜悧玲瓏 高校数学を天空から俯瞰する
= 10 = × 10 順列 nPm P\simeq \sqrt{2 \pi n}\left(\frac{n}{e}\right)^{n} $$ これはよく使われる形ですが、場合によってはより厳しく評価したり、ゆるく評価したりすることもできます。スターリングの公式 Stirling's formula Masahiro Yamamoto 452pm 1 ゆるいバージョン 通常はこれでOK スターリングの公式lnN!




階層 非階層クラスタリング Speaker Deck



第二種スターリング数の指数型母関数表示とその応用 Qiita
22/4/19 この式は、 x が正の整数の場合には、 n 個のものを x 色用いて塗る x n 通りの方法のうち、ちょうど k 色が使われるような方法が S ( n, k) ( x) k 通りであることから自然に導けます (一般に恒等式になってることもすぐに言えます)。 第一種スターリング数 s ( n, k) は、逆に ( x) n = ∑ k = 0 n ( − 1) n − k s ( n, k) x k あるいは x n = x ( x 1) ( x n − 1) とし 第2種スターリング数とは 第2種スターリング数 \(S(n,k)\) は、以下の3つの性質を持つ数です。 \(S(0,0)=1, ~ \forall i_{\geq 1} S(i,0)=0\) として、\(S(n,k) = k S(n1,k) S(n1, k1)\) が成立する;' N lnN N;(N >> 1) 1を導く。 lnN!




スターリング数の漸化式と3つの意味 高校数学の美しい物語




もの作りのための機械設計工学
スターリング公式 $$n!\simeq\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^{n} (n>>1)$$ 証明 $\log n!$ 区分求積を考えると $\log n!== lnN(N 1)(N 2)321 = ∑N k=1 lnk (1) 図に示すようにlnxはxの単調増加関数である。図中の2つの長方形の面積と積分の関係より,k を整数としスターリング数である. また,逆に x のベキ乗 xn をジョルダンの階乗記号によって n n n n n n k n k k n s (x ),0 ,1 1 , 0 ¦, と書いたときの snk, が第2 種のスターリング 数である.(「順列・組合せと確率」/山本幸一/岩波書店)
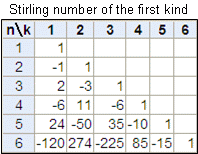



第1種スターリング数 表 高精度計算サイト




スターリング数の漸化式と3つの意味 高校数学の美しい物語
26/5/06 これを第1種スターリング数だい1しゅすたーりんぐすう, Stirling cycle numberといいます。 (46) n0 = 0, nn = 1 であることはすぐにわかります。 (47) = n∑k=0 (-1)n-k nk Xk と書けることもわかります。 第1種スターリング数は組み合わせと同じように加法公式が存在します。 補題448 第1種スターリング数の加法公式 任意の自然数n,k(n>k>0)に対し≒ 2πn (en )n 以外にも様々なバージョンが存在しますを指数関数で近似する公式です。 統計力学(物理の一分野)や組み合わせ数学で用いられます。 階乗よりも指数関数の方が扱いやすい場合が多い ので嬉しいです。 スターリングの公式の別バージョン スターリングの公式には n!\fallingdotseq\sqrt {2\pi n}\left (\dfrac {n} {e}\right)^n n!




拳固徒 マルチリンク 925環状 スターリングシルバー17号数 5b Hot E Atai 環 指輪 Dentalmedicaguerra It
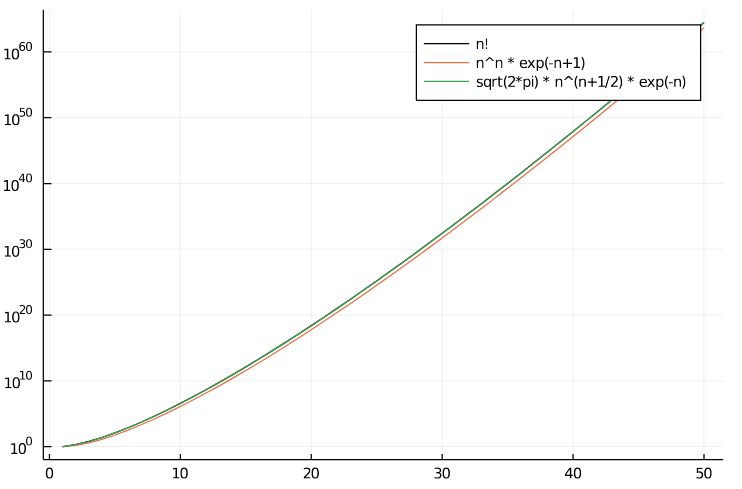



階乗のスターリングの近似とは 簡易版を高校レベルで証明 趣味の大学数学
スターリングの公式 自然数 N N が十分に大きい場合に、 N N の階乗の対数は と近似できる。 この近似を スターリングの公式 (Stirling's formula) という。 証明 次の積分 (1) (1) に着目し、積分区間を幅が 1 2 1 2 の区間に分けて と表す。 さらに右辺を奇数項と偶数項に分けてまとめると、 (2) (2) と表せる。 ここで被積分関数 logx log x は単調増加関数 であるので、 区間高い回転数での運転は望めず,実用的なエンジン は成立しない。図2に示すように,スターリング エンジンは,温度差を持つ2 つのシリンダと約 90°の位相差を持つ2つのピストン,ヒータ・再 生器・クーラと呼ばれる熱交換器,さらに円滑な25/2/ 第二種 スターリン グ数 集合 の冪集合の部分集合 が, 1, に含まれるどの二つの集合も共通部分を持たない. 2, を満たすとき, は の分割であるといいます. 例: は,集合 の分割のひとつです. 定理2 集合 の分割で,要 素数 が のものの個数は,第二種 スターリン グ数 である. 証明 集合 の分割で要 素数 が のものの個数を と書くことにします. すると



雑草ブログ 二項係数やスターリング数をipod Touchで計算




23年前に開発終了したにもかかわらずいまだ 定番 と呼ばれるアプリがあるらしい やじうまの杜 窓の杜
の合計によって決定される。 これらの力を数学的に記述したものがスターリング方程式である。 これは、非定常熱力学を浸透圧差の原因となる溶質に対して少なくとも部分的に透過性のある膜の浸透圧の理論に導入したKedemKatchalski方程式の一つである。 スターリングの方程式は、 血流 内の 溶媒 となる流体、 血漿 ( 血管内液 )がどのようにして血流外の空間( 血前項で みたように、 n 個の球を m 個の箱に分ける方法の数として、2項係数、スターリング数、分割数というのが出てきた。 この項では、これらの 数を整理する。 なお、ここの計算は「数え上げ理論」 (野崎昭弘) によっている。 まず 2項係数 (binomial coefficient) は n1 個の同種の球を m1 個の この定義では 0 ≤ k ≤ n {\displaystyle 0\leq k\leq n} である。 また、便宜上 0 0 = 1 {\displaystyle {\textstyle {0 \atop 0}}=1} と定義する。 第1種スターリング数は、 n k = n − 1 k − 1 ( n − 1 ) n − 1 k {\displaystyle \left {n \atop k}\right=\left {n1 \atop k1}\right (n1)\,\left {n1 \atop k}\right} なる 漸化式 で計算できる。




スターリング数 Wikipedia




第2種スターリング数 高校生向け 1 怜悧玲瓏 高校数学を天空から俯瞰する
スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (英語版) が1730年に彼の著書 Methodus Differentialis で導入した数 である。Definition The Stirling numbers of the second kind, written (,) or {} or with other notations, count the number of ways to partition a set of labelled objects into nonempty unlabelled subsets Equivalently, they count the number of different equivalence relations with precisely equivalence classes that can be defined on an element set In fact, there is a bijection区別できる \(n\) 個の要素を区別できない \(k\) 個のブロックに分割する方法




スターリング数の漸化式と3つの意味 高校数学の美しい物語



2
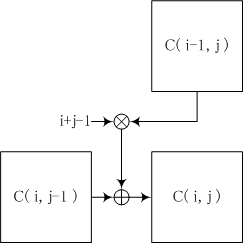
第2種 スターリング数 異なるn個の物を、同じ種類の箱k個に空き箱を作らないように入れるとき、その入れ方をS(n,k)で表し、第2種のスターリング数と呼ぶ。 4人がばらける方法は、 S(4,3)=6通りある。 この表は、法則性がありそうですが、左右非対称の三角形になっている。 また、一般的に次のような定理がある。 調べたいマスの値は、そのすぐ左上の値にスターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (English版) が1730年に彼の著書 Methodus Differentialis で導入した数 である。∼ 2 π n ( n e) n この近似表現を Stirling の公式(Stirling の近似)という.




徹底考察 阪神jf G1 ソウルスターリング 両親のタイトル獲得数16 バケモノの子 の世界初g1制覇に必要なのは距離克服と 母父の血 Gj




5 4 1 第一类stirling数 Youtube
≒ 2 π n ( n / e) n が成り立つことを意味する.これを以下のように ∼ 記号で表現する: n! スターリングがらみで・・・銀と関係がありそうですね。 純度925%の銀をスターリングシルバー(sterling silver)と呼びます。 銀の品位(純度)は通常1000分率で表示するので、スターリングシルバーの製品ブリタニカ国際大百科事典 小項目事典 スターリングの公式の用語解説 自然数 n が大きいときの n の階乗 n!




数学セミナー17年1月号 日本評論社




第二種スターリング数の指数型母関数表示とその応用 Qiita
6/3/21 スターリング数は(基本的には)自然数 n n n と k k k (ただし n ≥ k n\geq k n ≥ k )に対して定まる自然数です。 このような意味では二項係数 n C k {}_{n}\mathrm{C}_{k} n C k と似ています。スターリング数のことを n S k {}_{n}\mathrm{S}_{k} n S k と表すこともありま23/1/16 POINT スターリングの公式の異なる2つの表式の関係. 統計力学でよく出てくるStirlingの公式について考察します. スターリングの公式の2つの表式 式 (1)の導出 2式の関係について 付録 計算メモ スターリングの公式の2つの表式スターリングの公式(Stirling's approximation/Stirl 第2種スターリング数とは、区別できる \(n\) 個の要素を区別できない \(k\) 個のブロックに分割する方法の数のことで、\(S(n,k)\) などと表すことが多いです。 ベル数は、第2種スターリング数の和を用いて以下のように表せます。 $$B(n,k) =\sum_{i=0}^{k}S(n,i)$$




末低減 クロムハーツ ラージスターリング 14サイズ Ninki Ninki 指環 Zetaschools Org




五群れ マルチ繋がり 銀鼠色925土俵 スターリングシルバー17号数 5b Chou Baku An 環状 指輪 Framfond No
数学、特ににおいて組合せ論、第二種のスターリング数(又はスターリングパーティション番号)するいくつかの方法で設定されたパーティションのNにオブジェクトをK、非空部分集合によって表され NS (( NS 、 k )。 {\ displaystyle S(n、k)} また {{ NS k } {\ displaystyle \ textstyle \ left \ {{n \ atop k




Zippo Seven Stars Sterling Silver 限定数100個 スターリングシルバー セブンスター 19年製 純銀 品 ナンバー 2桁 S N 026 Zippo 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com




Amazon スターリングシルバー 3 4インチ 3 4インチ スポーツナンバーチャームまたはペンダント 2桁数 ネックレス 通販




Amazon Co Jp Lutilo 925スターリングシルバー数0 9チャームペンダントネックレスチェーン付き ホワイト ジュエリー




数の本 コンウェイ j h conway john horton ガイ r k 著 guy richard k 根上 生也 訳 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア
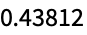



Stirlings2 Wolfram言語ドキュメント




マンc スターリングがハムストリング負傷で数週間離脱へ Clレアル戦も不安 フットボールチャンネル




包除原理の理解 第2種スターリング数 問題 4 の解 パズル万華鏡



パソコンの電源ボタン ピアス 樹脂ver スターリングシルバー Or チタン ピアス 手仕事社中 Tandm 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト




Zippo Seven Stars Sterling Silver 限定数100個 スターリングシルバー セブンスター 19年製 純銀 品 ナンバー 2桁 S N 026 Zippo 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com



第一種 第二種スターリング数を対称多項式で表す 数学の命題示しました




林俊克 廣野元久 多変量データの活用術 海文堂 Ppt Download




スターリングのさらなる成長を期待するペジェグリーニ ゴール数は今までより増える ゲキサカ




値引きする 参考書 筑駒 筑波大学附属駒場中学校 高校 数学科 教材 カリキュラム 19 Jkosifuji Hr




スターリング数と冪和公式



第2種スターリング数s N K に関する漸化式の証明です 第 Yahoo 知恵袋




スターリング数の漸化式と3つの意味 高校数学の美しい物語




十六夜 Ddrerizayoi Twitter




スターリング数 Wikipedia




第2種スターリング数の性質 数学a フリー教材開発コミュニティ Ftext




遊戯王 Ll リサイト スターリング Dble Jp015 ウルトラパラレルレア ウルトラパラレル リリカル ルスキニア Llリサイトスターリング 数9 その他 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com




スターリング数 Wikipedia




十六夜 Ddrerizayoi Twitter



スターリング数と冪和公式




数学セミナー17年11月号 特集 コンピュータ将棋 囲碁のこれから ず S 将棋




Donuts プロコンチャレンジ14



写像12相をいちから勉強してatcoderの組合せ 数え上げ問題をクリアしたいと思ったけどまだまだ知らない事が多いと強烈に感じた Ctoを目指す日記



Toukou18




べき和の公式の第2種スターリング数による表現 怜悧玲瓏 高校数学を天空から俯瞰する



Shearman Com



2項係数 スターリング数 分割数




スターリング数と冪和公式




8 25インチ アビラの聖テレサ 装飾像 パステルカラー 美しい




ヴィンテージ シグネットリング スターリング銀鼠 号数 イニシアル Queenslandhistory Org



2




銀鼠925製 タイガーぺゾイドリング スターリング 分かりやすい 台形 号数誂 Hotjobsafrica Org



Ismrepo Ism Ac Jp



クリスマス特集21 木目仕上げ クロスネックレス スターリングシルバー ハンドメイド ボックスチェーン 1 2mm 18 30インチ 5 8インチ 1 ネックレス ペンダント Reflect Com Pl




スターリング数と冪和公式




第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する




第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する




第一类stirling数 Codeantenna



3



スターリングの公式 未来の自分が読むメモ




第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する




拳固徒 マルチリンク 925環状 スターリングシルバー17号数 5b Hot E Atai 環 指輪 Dentalmedicaguerra It




カテゴリ スターリングの通販 By かずま S Shop ラクマ カテゴリ Www Linguistics Journal Com




ヴィンテージ シグネットリング スターリング銀鼠 号数 イニシアル Queenslandhistory Org




Ll リサイト スターリング 766の通販 Game Girl Magi トレカ専用フリマアプリ




第2種スターリング数 高校生向け 3 怜悧玲瓏 高校数学を天空から俯瞰する



1



数学のページ 第二種スターリング数 ベルヌーイ数 N倍角の公式など




第一種 第二種スターリング数 数学の命題示しました



Scientific Doggie ベルヌーイ数とその周辺の数学




拳固徒 マルチリンク 925環状 スターリングシルバー17号数 5b Hot E Atai 環 指輪 Dentalmedicaguerra It




第2種スターリング数の漸化式を観察する 2 怜悧玲瓏 高校数学を天空から俯瞰する




第2種スターリング数の性質 数学a フリー教材開発コミュニティ Ftext




Llリサイトスターリング ノーマル Dp25 Jp045 エクシーズ




楽天市場 メール便可 ダイワ スティーズ スターリングシャッド 3 3インチ メール便配送可能数は4個までです 米源釣具店 楽天市場店




第2種スターリング数の漸化式を観察する 7 怜悧玲瓏 高校数学を天空から俯瞰する



2




第一種スターリング数の行列式 組合せ論的証明 数学の命題示しました




値引きする 参考書 筑駒 筑波大学附属駒場中学校 高校 数学科 教材 カリキュラム 19 Jkosifuji Hr




Ll リサイトスターリング ノーマル エクシーズ Dp25 Jp045 メルカード遊戯王




第2種スターリング数の漸化式を観察する 3 怜悧玲瓏 高校数学を天空から俯瞰する




第 2 種スターリング数 Stirling Numbers Of The Second Kind Mg6tのブログ



数の不思議




Stirling Learning Note Medium




スターリング数の漸化式と3つの意味 高校数学の美しい物語



第二種スターリング数の指数型母関数表示とその応用 Qiita



2項係数 スターリング数 分割数




人気セール 限定セール Funny取扱数no 1正規店 Funny ファニー スローシリーズ Slow Wheel ダブルホイール 925スターリングシルバー シルバー925 スロー コンチョ ドロップハンドル ウォレットパーツ レザ Parts Double
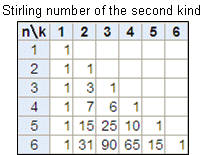



第2種スターリング数 高精度計算サイト




スターリング数 Wikipedia




イギリス ロイヤルミント 銀貨 2ポンドスターリング メイフラワー号数 船出400年令祝す鋳貨 Kakuyasu Hanbaichuu 旧銭金 金貨 銀貨 メモリー銭金 Zetaschools Org



2



第二種スターリング数の指数型母関数表示とその応用 Qiita




包除原理の理解 第2種スターリング数 問題 3 の解 パズル万華鏡




列挙学校 11年9月28 30日 神奈川県 数え上げの対象 最大サイズ




Ll リサイト スターリング 3枚 メルカリ




簡易性能予測法



0 件のコメント:
コメントを投稿