Y = 2 Hence x = 3, y = 2 (b) 3x y = 10 Since we have one equation and 2 variables, it cannot be solved by elimination method To solve this, we can go for trial and error Say y = 1, x = 3 or x = 5, y = —5 (c) x – 3y=1 eq 1 3x – 2y 4 = 0 eq 2 Multiply eq 1 by 3, 3x — 9y = 3 eq 3Example 5 Solve the system of linear equations using the GaussJordan elimination method 7y 5z 12 x 2y 3z 3 y 8z 9 − = − =− − = Math 1313 Section 32 Example 6 Solve the system of linear equations using the GaussJordan elimination method 3x 4y 4z 19 x 2y 3z 7 2x 4y 6z 38Which method do you use to solve the system of equations #y=1/4x14# and #y=19/8x7#?
Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Ii X 2 2y 3 1 And X Y 3 3 Sarthaks Econnect Largest Online Education Community
X+2y=3/2 2x+y=3/2 by elimination method
X+2y=3/2 2x+y=3/2 by elimination method- The Questions and Answers of Solve using substitution method 3x/25y/3=2 , x/2 y/2=13/6?ans x=2,y=3?Solve the Given equation in Elimination method and Substitution Method




0 0 0 0 6 Solve The System Of Linear Equations Chegg Com
1 Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 (ii) 3x 4y = 10 and 2x – 2y = 2 (iii) 3x – 5y – 4 = 0 and 9x = 2y 7 (iv)Solve the system by the elimination method 2x y 4 = 0 2x y 4 = 0 When you eliminate y, what is the resulting equation?Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y = 12x 21y =
\(x y = 5 \\2x 3 y= 4 \) Steps Elimination methodX2y = 3 (2) Multiply (2) by 7 to get 7x14y = 21 (3) Eliminate 7x by subtracting (3) from (1) 15y14y = y = 2–21 = 19 Hence y = 19 From (2), x = 3–2y = 338 = 41 Hence x = 41, y =4x312x2y9xy2 Final result x • (2x 3y)2 Step by step solution Step 1 Equation at the end of step 1 ((4•(x3))((12•(x2))•y))32xy2 Step 2 Equation
3x y = 7 Solution 2x – y = 3 (1) 3x y = 7 (2) The coefficient of y in the 1st and 2nd equation are same (1) (2) 2x – y = 3 3x y = 7 5x = 10 x = 10/5 = 2 By applying the value of x in (1), we get 2(2) y = 3 Pick either one of the equations and make either x or y the subjects of the formula and substitute the value of either y or x into the other equation Ie " "x=32y" " (from first equation) Now substitute x above into second equation 2(32y)y=1 64yy=1 65y=1 5y=7 Therefore y=7/5 Now substitute the yvalue into the equation to find x 2x7/5=1 2x=5/5(=1) 7/5 x=1/5 Thus, xGiven data The first equation is 2x3y = 1 2 x 3 y = 1 The second equation is 4x6y =2 4 x 6 y = 2 The second equation can be also written as, See full answer below




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Solved By Elimination Method 7x 15y 2 And X 2y 3 Brainly In
Question Solve The System By The Method Of Elimination {2x 5y = 11 5x 7 = 19 {3x 2y Z = 0 6x 2y 3z = 2 3x 4y 5z = 5 {x 4y Z = 3 2x 5y Z = 0 3x 3y 2z = 1 Find The Equation Of The Parabola Y = Ax^2 Bx C That Passes Through The Points (0, 6), (2, 2), And (3, 9/2) In Exercises 8 And 9, Write The Partial Fraction DecompositionSolve by the method of elimination (i) 2x – y = 3; Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 x




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In




X 2y 3 2 2x Y 3 2 By Substitution Method Novocom Top
How do you solve #12y3x=1# and #x4y=1# using the substitution method? Find an answer to your question Use the elimination method 1) 3xy=1 5xy=9 2) 4x6y=24 4xy=10 3)2xy=3 x3y=16 4) 2x3y=7 3x4y=10Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Ii X 2 2y 3 1 And X Y 3 3 Sarthaks Econnect Largest Online Education Community For more information and source, see on this link https



The Elimination Method




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In
10 Solve by elimination method 2r5s = 7 5r2s=55 11 is the pair parallel, perpendicular, or neither 5x2y=4 2x5y=10 12 Solve by the elimination method 2x3y = 3 4x6y= 6 16 Solve by the subsit read moreElimination method 2x5y = 3 > (1) 2x2y = 6 > (2) To eliminate the x value subtrat equation (2) from (1) 2x5y = 3 2x2y = 6 () () () _____ 3y = 9 Divide to each side by 3 3y/3 = 9/3 ⇒ y = 3 Substitute the y value in (1) 2x5*3 = 3 2x15 = 3 Add 15 to each side 2x1515 = 315 2x = 12 Divide to each side by 2 2x/2 = 12/2 ⇒ x = 6 Solve each of the following systems of equations by the method of crossmultiplication a^2x b^2y = c^2 b^2x a^2y = a^2 asked Apr 27 in Linear Equations by Gargi01 (k points) pair of linear equations in two variables;




Graph Graph Inequalities With Step By Step Math Problem Solver




Chapter 5 Review Exercises
Question solve the following simultaneous equations using elimination method, x2y3=6 2x3y46xy=4 Answer by math_helper(2163) (Show Source) You can put this solution on YOUR website!Substitution Method in Algebra!HELP PLZ!Multiply the both sides of the second equation by 2 Distribute and multiply Now add the equations together You can do this by simply adding the two left sides and the two right sides separately like this Group like terms




Solving A System Of Equations Using A Matrix Precalculus Socratic




Solve 3x Y 2z 12 X 2y 3z 11 2x 2y Z 2
Question 2 Solve the system i2x y 0, y2y 3 2 sin t, by using the elimination method (operator method) NB Eliminate x firstExplain each step as it is performed 5y = x 2x 3y = 7 Would the elimination method have been your first choice to solve this problem?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
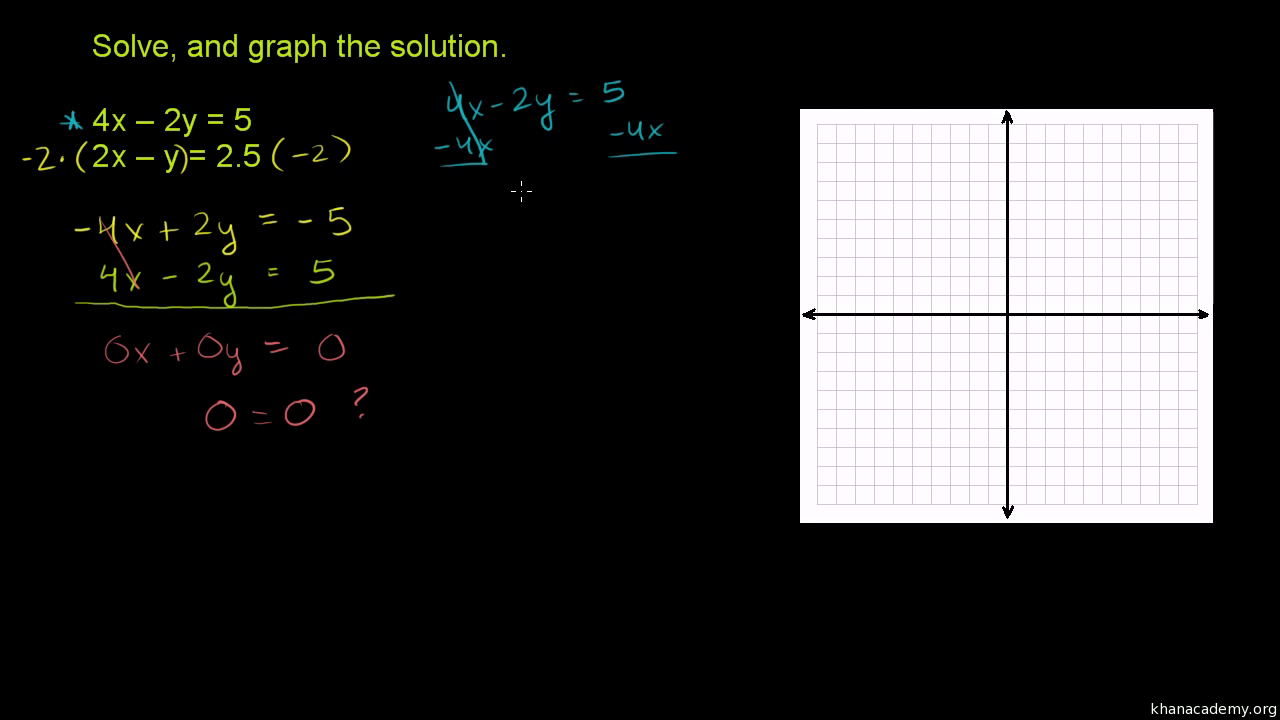



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




123a Ppt All 2
SOLUTION using elimination method solve problem 3x2y=1 4xy=6 You can put this solution on YOUR website!4x = 8 1) 2x y = 3 2) x 2y = 1 If equation 1 is multiplied by 2 and then the equations are added, the result is 3x = 5 Solve the system by the elimination method Check your workSolution Step 1 Select a variable which you want to eliminate from the equations Let us select y y 4x−3y = 32 xy = 1 4 x − 3 y = 32 x y = 1 Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of




Simultaneous Equations 1 Ppt Download



Q Tbn And9gcrzricqcbiwggjbvlifkaeqo Mbnicdskvd Z9bnfr79bjrnvbg Usqp Cau
X/2 2y/3 = 1 and xy/3=3 Find x and y values using Elimination and Substitution method x/2 2y/3 = 1 and xy/3=3 Find x and y values using Elimination and Substitution methodMath 11 When using an elimination strategy to solve the system 3a^2=175t and 7a24=3a^22t, the variable that can be eliminated is A a B a^2 C t D an elimination strategy cannot be used with this systemX 2(4) 4 = 3 x 8 4 = 3 x 4 = 3 x = 1 So, the solution is (1, 4, 4) Question 2 Solve the following systems of linear equations by Gaussian elimination method 2x 4y 6z = 22, 3x 8y 5z = 27, − x y 2z = 2 Solution




X 2y 3 2 2x Y 3 2 By Substitution Method Novocom Top




Solving Linear Equations Using Gaussian Elimination Method
Click here👆to get an answer to your question ️ Solve by elimination method x y = 5 2x 3y = 4 Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables > Algebraic Methods of Solving a Pair of Linear EquationsStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x=2y3;2x3y=5 Tiger Algebra SolverWhat are the 2 numbers if the sum is 70 and they differ by 11?




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy
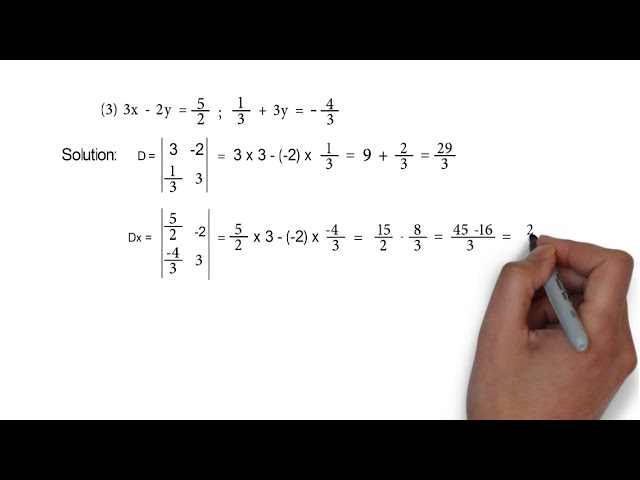



3x 2y 5 2 And 1 3 3y 4 3 Problem Set 1 Q5 3 Linear Equation In Two Variables Youtube
Or click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding orQuestion 10 Solve the following equations by the method of elimination by equating the coefficients x 2y = 3/2 2x y = 3/2 Solution Given, x 2y = 3/2 (i) 2x y = 3/2 (ii) Multiplying equation (i) with 2, 2x 4y = (3/2) × 2 2x 4y = 3 (iii) Subtracting (ii) from (iii), 2x 4y (2x y) = 3 – (3/2) 4y – y = (6 – 3)/2 3y = 3/2 by using elimination method 7x 15y = 2 (1) x 2y = 3 (2) 7(x) 7(2y) = 3*7 (multiplying the both numbers by 7) (3) subtracting the equation (3) from (1) 29y = 19 y = 19/29 putting the value of y in equation (2) x 2 * 19/29 = 3 x = 29*3/19*2 = 87/38 ANS




Solve The Following Pair Of Linear Equations By The Elimination Method The Substitution Method And Geometrical Method Frac X 2 Frac 2y 3 1 And X Frac Y 3 3 Snapsolve




2x Y 3 3x Y 7 Solve The Method Of Elimination Brainly In
The given system of equation is `x 2y = 3/2` ` (i) `2x y = 3/2` (ii) Let us eliminate y from the given equations The Coefficients of y in the given equations are 2 and 1 respectively The LCM of 2 and 1 is 2 So, we make the coefficient of y equal to 2 in the two equations Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label the equations Label the equations A and B (A) 3x 2y = 4 (B) x 4y = 3 Step 2 Isolate one of the variables To use the substitution method, we need to isolate one of the variables We will isolate variable x in equation B in this example xAnswer (1 of 2) Start by putting both equations in standard formfirst equation 2(xy) = 3x 2x 2y x = 3 (expand the parentheses, subtract x from both sides) x 2y = 3 (collect terms)second equation x = 3y 4 x 3y = 4 ;(subtract 3y from both sides)Now we can see that the coefficient of x is the same for both equations, so we can do "elimination" by subtracting one



The Equations Of Four Lines Are Given X 2y 3 0 3x 4y 7 0 2x 3y 4 0 And 4x 5y 6 0 What Can Be Said About The Four Lines Quora




Solved Solve The System Using The Elimination Method X Chegg Com
Another way of solving the system of equations is by Elimination method The solution of the set of equations x2y=3 and 2xy=6 is (3,0) Approved by eNotes Editorial TeamAre solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 If the answer is not available please wait for a while and a community member will probably answer this soonFree system of equations elimination calculator solve system of equations unsing elimination method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more elimination x2y=2x5, xy=3 en Related Symbolab blog posts Middle School Math Solutions



How To Solve The Following System Of Equations Using The Gauss Jordan Method X 2y Z 3v W 2 2x 4y 2z 6v 3w 6 X 2y Z V 3w 4 Quora




Given The Four Lines With The Equations X 2y 3 0 3x 4y 7 0 2x 3y 4 0 4x 5y 6 0 Then Youtube
1answer Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient x 2y = 3/2, 2x y = 3/2 askedin Linear Equations in Two Variablesby HarshKumar(327kpoints) linear equations inSolve by Substitution 3xy=2 , x2y=3 3x y = 2 3 x − y = 2 , x 2y = 3 x 2 y = 3 Subtract 2y 2 y from both sides of the equation x = 3 2y To find value of x & y by elimination method 2x 4y = 3 (1) 4x 2y = 3 (2) Do this to eliminate x, 2 × eqn (1) eqn (2) 4x 8y ( 4x 2y ) = 6 3 8y 2y = 3 6y = 3 Do this to eliminate y, 2 × eqn (2) eqn (1) 8x 4y ( 2x 4y ) = 6 3 8x 2x




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube




Example 7 Solve By Substitution 7x 15y 2 X 2y 3
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreQuestion 1 Solve the following pair of linear equations by the elimination method and the substitution method x y =5 and 2x –3y = 4 3x 4y = 10 and 2x – 2y = 2Solve the following systems of equations x 2y = 3/2 2x y = 3/2 asked Apr 26 in Statistics by Haifa (k points)




7 Solve The Following System Of Linear Equations Chegg Com




1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Respected Teachers Please Find The Value Of X And Y Mathematics Topperlearning Com 5qbsqgee
Ex 36, 1 Solve the following pairs of equations by reducing them to a pair of linear equations(i) 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6Let 1/𝑥 = u 1/𝑦 = v So, our equations become1/2 u 1/3 v = 2 (3𝑢 2𝑣)/(2 × 3) = 2Solve by Addition/Elimination x2y=3 2x3y=9 x − 2y = 3 x 2 y = 3 2x − 3y = 9 2 x 3 y = 9 Multiply each equation by the value that makes the coefficients of x x opposite (−2)⋅ (x−2y) = (−2)(3) ( 2) ⋅ ( x 2 y) = ( 2) ( 3) 2x−3y = 9 2 x 3 y = 9 Simplify Tap for more steps Simplify ( − 2) ⋅ ( x − 2 yAnswer to Solve the system by the method of substitution a) y = 2x^2 y = x^4 2x^3 b) x^2 y^2 = 169 3x 2y = 39 By signing up, for Teachers for Schools for Working Scholars® for College
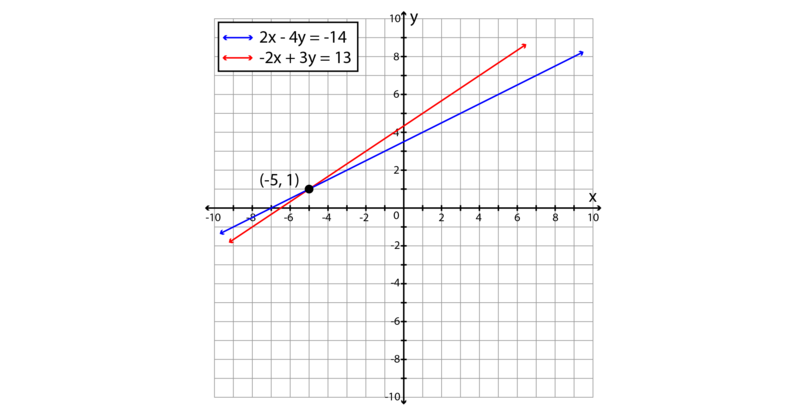



Elimination Method Simultaneous Linear Equations Siyavula




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
Elimination method x2y=2x5, xy=3 \square!Elimination method First multiply one or both the equations by some suitable nonzero constants to make the coefficients of one variable numerically equal then add or subtract one equation from the other so that one variable gets eliminated (i) What is the Known?Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!
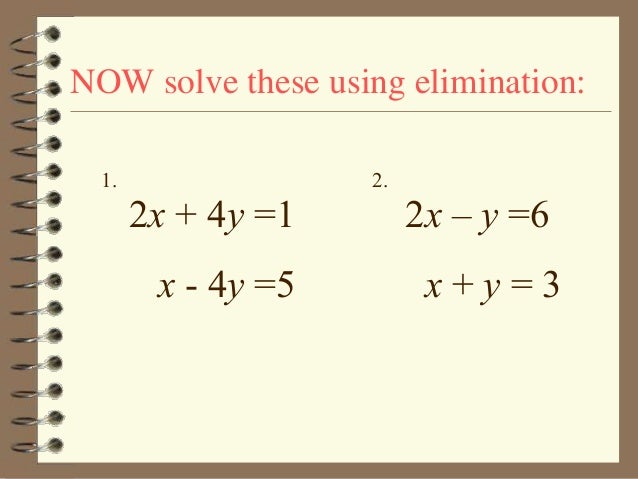



Wlh9cprf3s2b0m



1
Selina solutions for Concise Mathematics Class 9 ICSE chapter 6 (Simultaneous (Linear) Equations (Including Problems)) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear yourThe taxi fare in city is as follows For the first kilometer , the fare is Rs and for the subsequent distance it is Rs9 per km Taking the distance covered as x km and total fare as Rs y , write a linear equation for this information , and draw its graph , find the fare , 8x y z = 9, 2x 2y 3z = 22 and x 3y 2z = 15 solve for an ordered tripple asked in ALGEBRA 2 by harvy0496 Apprentice systemofequations




The Solution Of 2x Y Z 1 X 2y 3z 1 3x 2y 4z 5 Is 1 1 2 3 2 1 2 3 3 1 3 2 4 Youtube




Solving System Of Linear Equations Ppt Download




7 Solve The Following System Of Linear Equations Chegg Com




Solve 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 1 5 3x 2y 61 60 Mathematics Topperlearning Com 56o23roo



Solve The Following Systems Of Equations X 2y 3 2 2x Y 3 2 Sarthaks Econnect Largest Online Education Community




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




7 Solve The Following System Of Linear Equations Chegg Com




X 2y 3 2 2x Y 3 2 By Substitution Method Novocom Top




Solve Equations Using Substitution Method 2x Y 3 And 4x Y 3



Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Ii X 2 2y 3 1 And X Y 3 3 Sarthaks Econnect Largest Online Education Community




How Do You Solve The System 3 4 X 1 2 Y 1 2 And X Y 3 2 Socratic



1
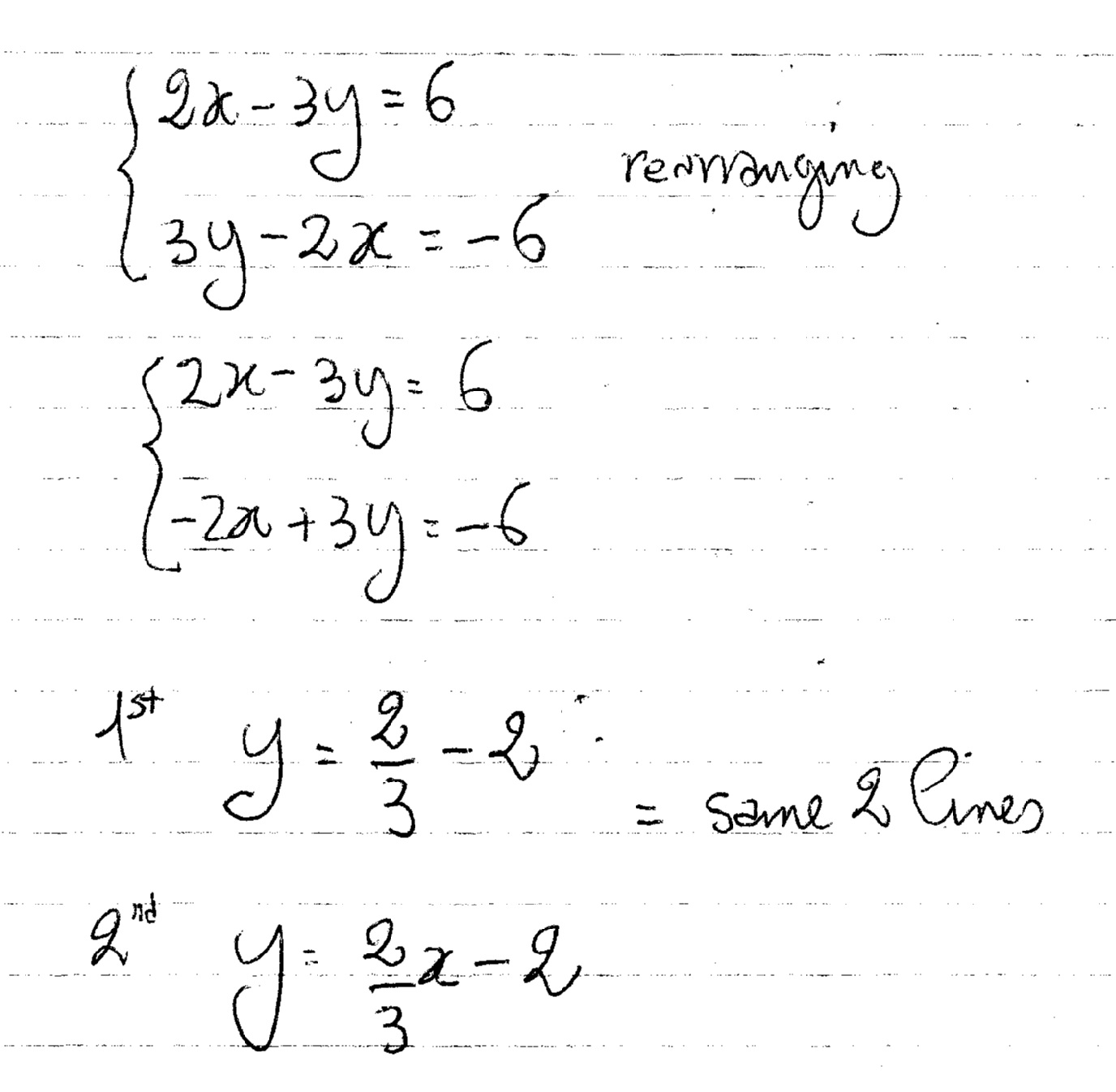



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline
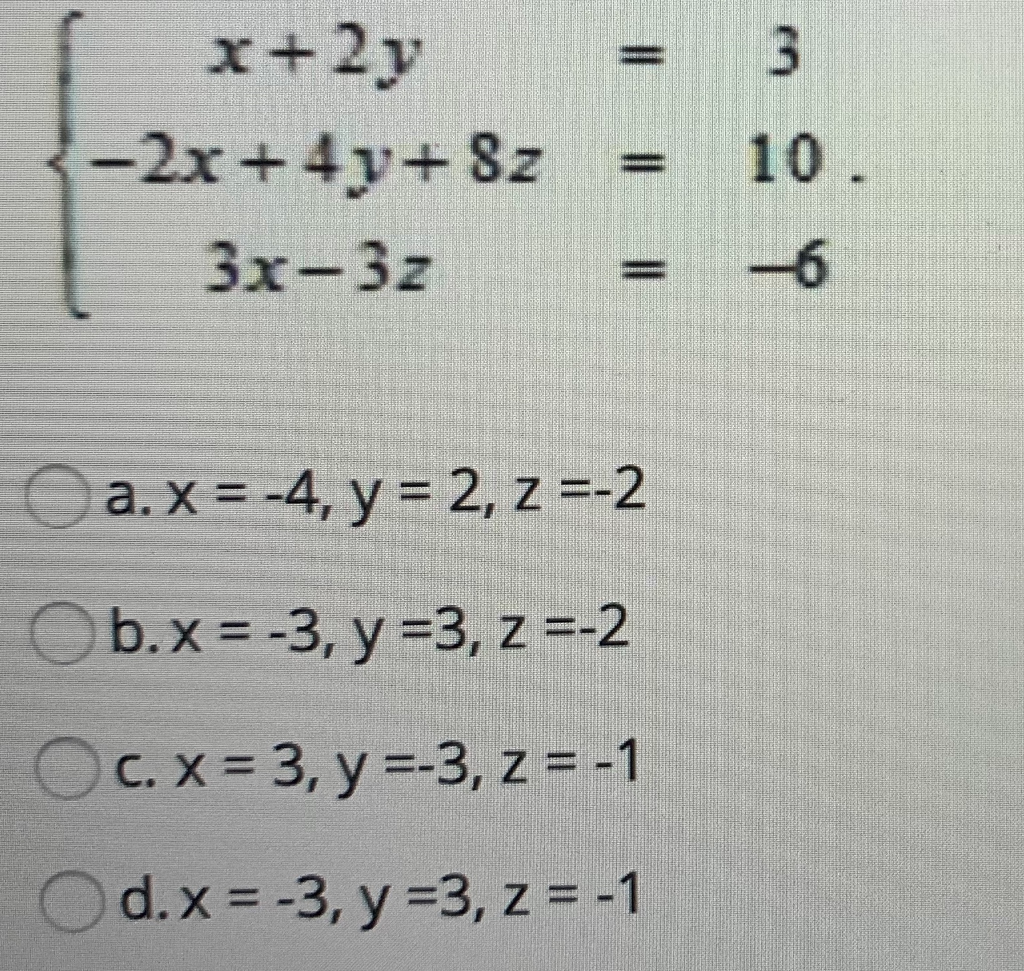



Use Gaussian Elimination Method To Solve The System Chegg Com




X 2y 3 2 2x Y 3 2 Find The Valve Of X And Y Brainly In



Ch 3 2



Solve The Following Systems Of Linear Equations By Gaussian Elimination Method I 2x 2y 3z 2 X 2y Z 3 3x Y 2z 1 Sarthaks Econnect Largest Online Education Community



Solve The Following Systems Of Linear Equations By Gaussian Elimination Method I 2x 2y 3z 2 X 2y Z 3 3x Y 2z 1 Sarthaks Econnect Largest Online Education Community



Systems Of Linear Equations




無料ダウンロード 3x 2y5 X5 Y




Solve 3x 2y 11 And 2x 3y 4




1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y




0 0 0 0 6 Solve The System Of Linear Equations Chegg Com




Example 5 Solve The System By Elimination X 3 2 Y Chegg Com




Solve The Following Linear System Of Equations By Chegg Com




X 2y 3 2 2x Y 3 2 By Elimination Method Brainly In




Example 7 Solve By Substitution 7x 15y 2 X 2y 3
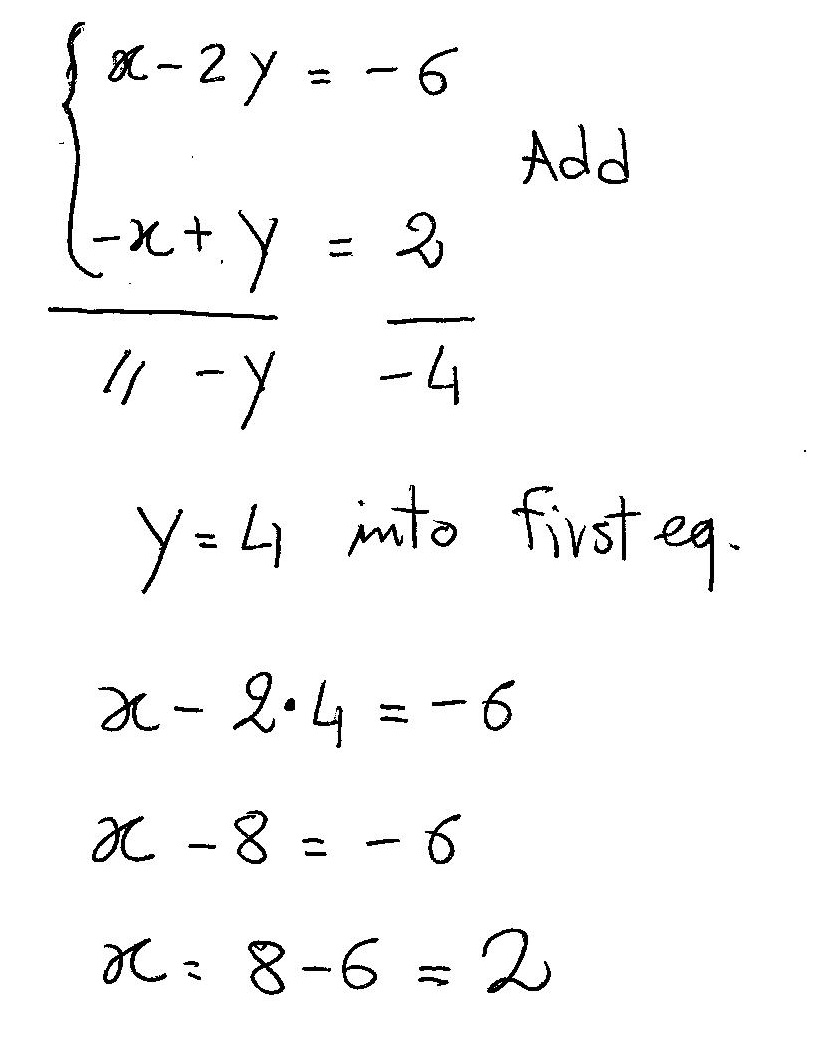



How Do You Solve X 2y 6 And X Y 2 Socratic




Solve Each Other Pair Of Equation Given Below Using Elimination Method 2y 3 X 12 5y 7 X 1 Mathematics Topperlearning Com D2p1cokk




2x 3 Y 3z 5 X 2y Z 4 3x Y 2z 3 Youtube




X 2y 4 6 Solve The System By Elimination 2x Y Chegg Com




Math 163 Online Problems Supplemental Lessons On Gaussian




Exercise 1 5 Matrix Gaussian Elimination Method Problem Questions With Answer Solution




1 Solve The Following Using Graphical Method 12 Chegg Com




Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube




Solve X 2y 1 2x Y 7 Maths Questions




Solve Using Substitution And Elimination Method 3x 2 5y 3 2 And X 3 Y 2 13 6 Brainly In



If X Y 3 X Y 1 Then What Is X Y Quora



1




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Cbnst 1 Science Software Equations



Solved In Exercises 17 24 Solve The System Of Linear Equations Using The Gauss Jordan Elimination Method 2x 3y 5 18 3x 2y 3 3x 4y 1 Course Hero



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community



Exercise 1 Solve The Following Using Gauss Chegg Com




Solve The Following System Of Linear Equations By Matrix Method X Y Z 3 2x Y Z 2 X 2y 3z 2 Youtube




X 2y 3 2 2x Y 3 2 By Substitution Method Novocom Top



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community



Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection




Solve By Matrix Method X 2y 2 2x 3y 3 Good Example Part 1 Youtube




2x 2y 3 2x 3y 8 Solve By Elimination Method Brainly In



If X Y 3 X Y 1 Then What Is X Y Quora




2x 3y 8 X 2y 3 0 By Substitution Method Brainly In




Elimination Method Day 1 Ppt Download
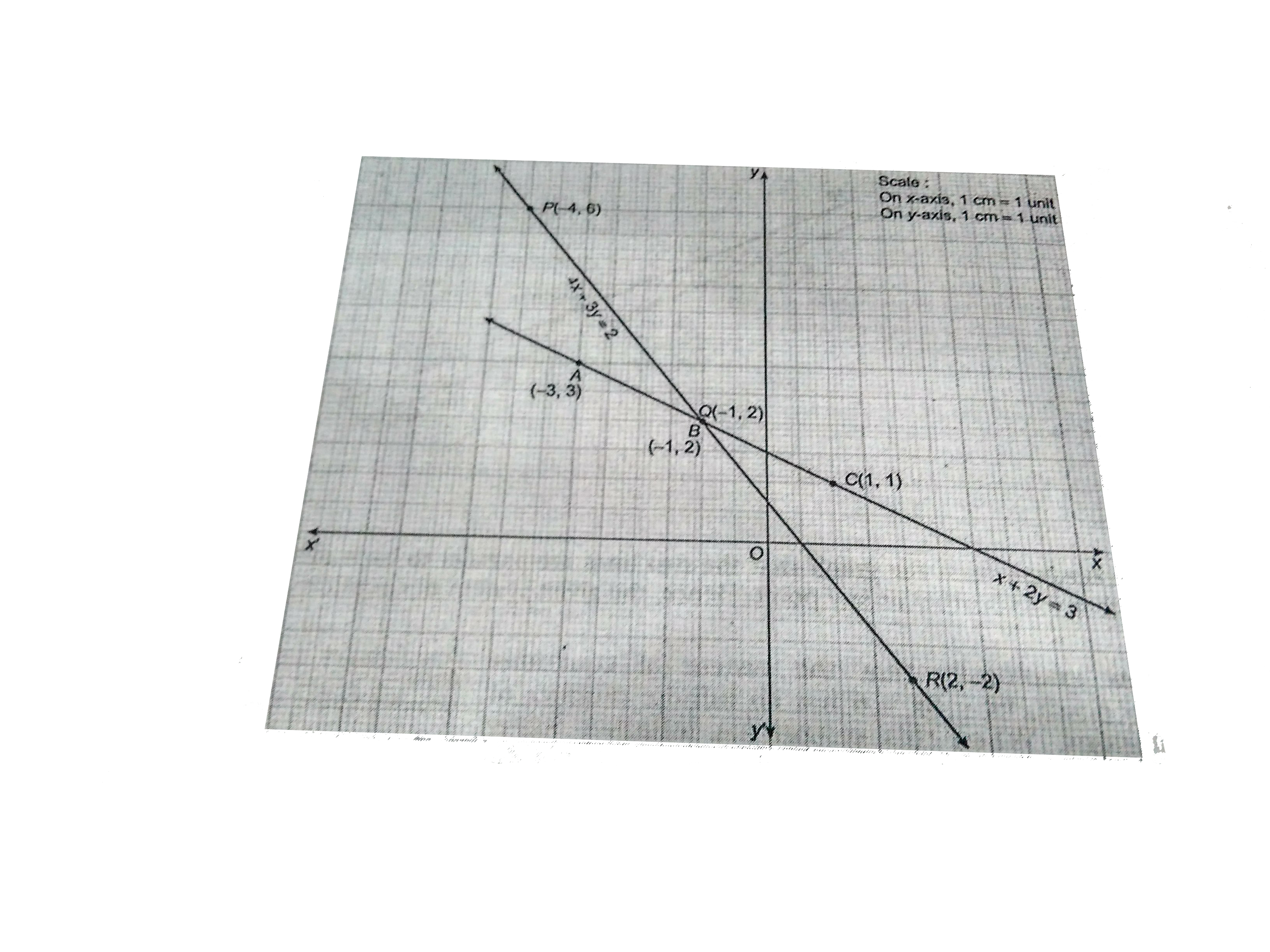



Show Graphically The System Of Linear Equations Br X 2y




Solve Systems Of Equations By Elimination Ppt Download
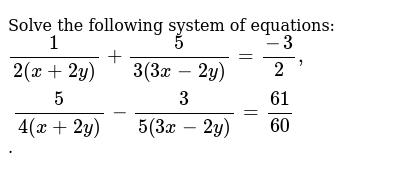



Solve The Following System Of Equations 1 2 X 2y 5 3 3x 2




Answered Find Any Four Ordered Triples That Saui Bartleby




Please Answer Question 2 Olve For X And Y 7 Y 3 2 14 C A 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Wlh9cprf3s2b0m




Solving A System Of Equations Using A Matrix Precalculus Socratic




X 2y 3 2 And 2x Y 3 2 By Elimination Method Brainly In




7 Solve The Following System Of Linear Equations Chegg Com




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




X Y 6 X Y 2 By Elimination Method Novocom Top




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




X 2y Z 3 2x 3y 3z 10 3x Y 2z 13 Solve By Gauss Elimination Memod




Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination



0 件のコメント:
コメントを投稿