· 首先我们来证明蓝色点组成的是一个独立集:如果有两个蓝色点间有边相连,那么这条边则没有被覆盖,则与条件1矛盾。因此是独立集。 再来证明这个独立集最大: 如果我们要再增加这个独立集中的点,则需要把某个红点变成蓝点。最小点覆盖 最小点覆盖:大小最小的一个点集,让每条边都至少和其中一个点连接; 二分图的最小点覆盖=最大匹配数 略证:金海峰的博客 最小边 · 这篇文章讲无权二分图(unweighted bipartite graph)的最大匹配(maximum matching)和完美匹配(perfect matching),以及用于求解匹配的匈牙利算法(Hungarian Algorithm);不讲带权二分图的最佳匹配。 二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。
二分图的最大匹配 最小顶点覆盖 最大独立集等价的线性规划证明 知乎
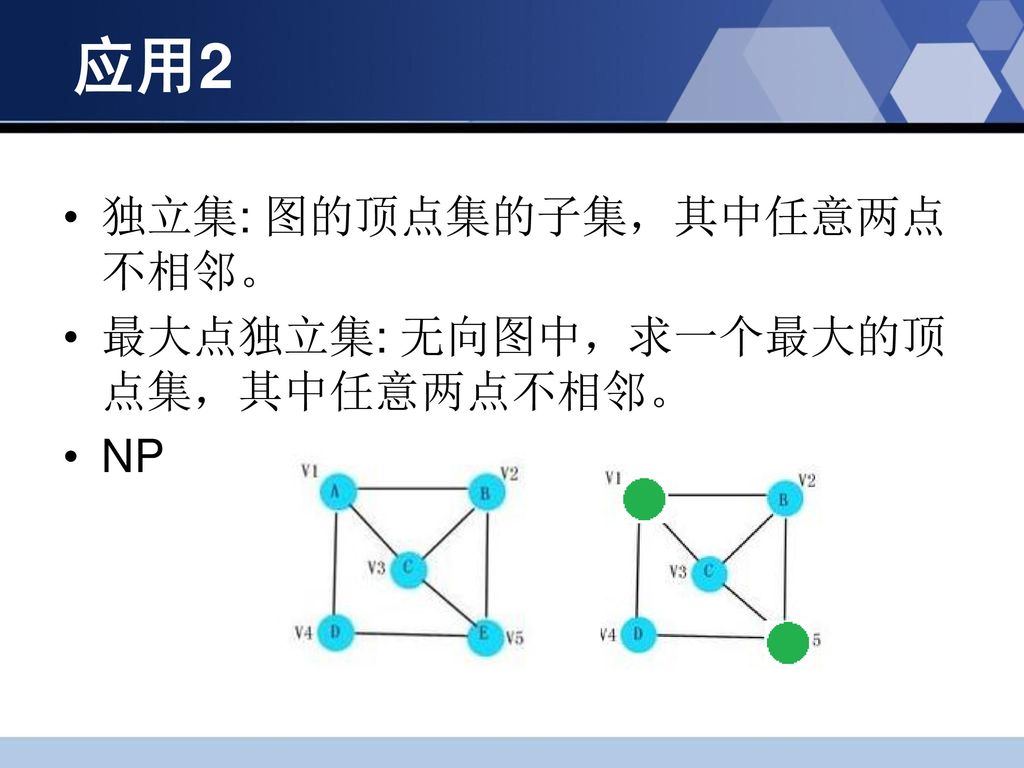
二分图最大独立集
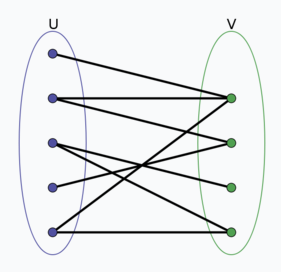
二分图最大独立集- · 独立集、极大独立集 独立集即一个点集,集合中任两个结点不相邻,则称V为独立集。或者说是导出的子图是零图(没有边)的点集。极大独立集(maximal independent set):本身为独立集,再加入任何点都不是。最大独立集(maximum independent set):点最多的独立集。 · 二分图最大独立集 先说一下什么是二分图的最大独立集:就是在二分图中选尽量多的点,但得保证选出的点中任意两点之间没有边。举个例子,如下图。 红色点就是最大独立集中的点,我们可以看到这些点两两之间都没有边相连。



Oi之路 04图论 9二分图 Zory的个人博客
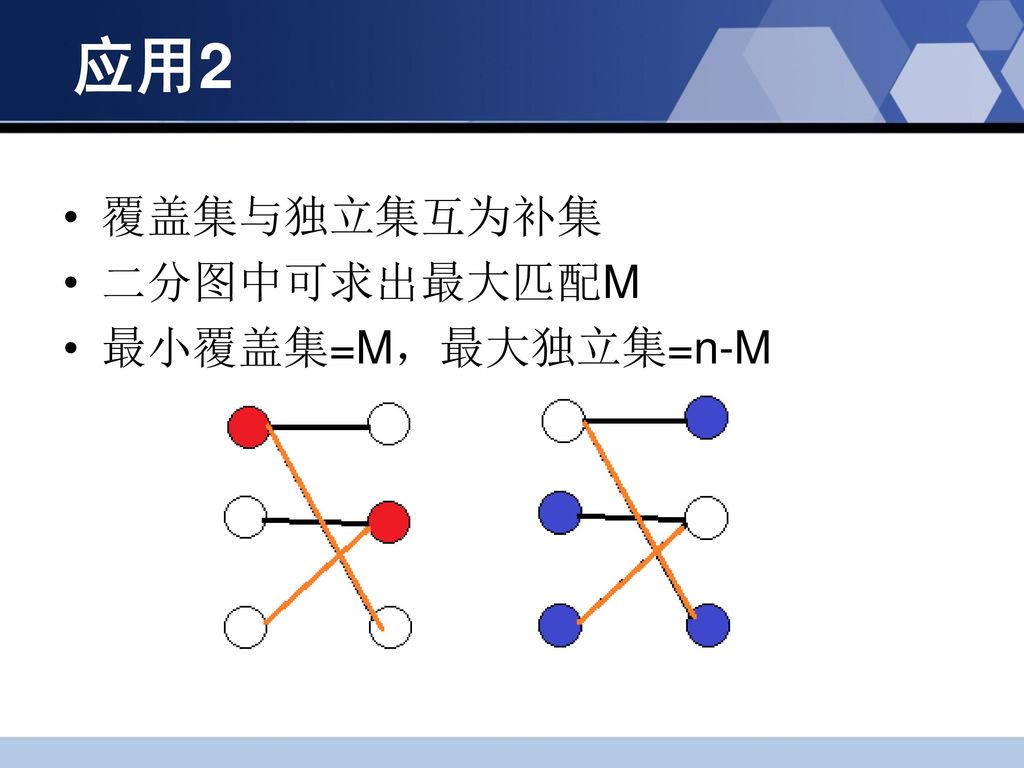
· 一个独立集是极大独立集,当且仅当它是一个支配集。 定理3 设无向图g(v, e)中无孤立顶点,顶点集合v*⊆v,则v*是g 的点覆盖,当且仅当v–v*是g 的点独立集。 推论 设g 是n 阶无孤立点的图,则v*是g 的极小(最小)点覆盖集,当且仅当v–v*是g的极大(最大)点 · 最大独立集合的定义 是 最大无关系点的集合。 而 最小点覆盖的定义 是,二分图中每个边至少一个端点在该点集中 的 最小点集。 · 二分图的最大独立集 如果一个图是二分图,那么它的最大独立集就是多项式时间可以解决的问题了 最大独立集 = V最大匹配数 证明:
二分图问题资料整合处理(1):"支配集覆盖集与独立集" BelowLuminous edited 3 年,10 月前 各种定义 一、点支配 支配 对于图G中顶点集合V中的某一个点A与另一个点B有边链接,叫做点A支配B。二分图最大点权独立集 最小割 j 餐巾计划问题 线性规划网络优化 最小费用最大流 k 航空路线问题 2条不相交路径最大长度 最小费用最大流 l 软件补丁问题 最小转移代价 最短路 m 星际转移问题 网络判定问题二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
题目列表 模板二分图最大匹配 ZJOI07 矩阵游戏 ZJOI09假期的宿舍 飞行员配对方案问题 最小路径覆盖问题 USACO05JANMuddy Fields G 国家集训队部落战争 TJOI13攻击装置 · 最小边覆盖 = 最大独立集 = V 最大匹配数 这个是在原图是二分图上进行的 最小路径覆盖和最小边覆盖不同,不要求给的图是二分图,而是要求是N x N的有向图,不能有环,然后根据原图构造二分图,构造方法是将点一分为二,如,i分为i1和i2然后如果i和j有边,那么就在i1和j2之间连一条边。 · 匈牙利算法详解 把一个图的顶点划分为两个不相交的集合 U 和 V ,且使得每一条边都分别连接 U 、V 中的顶点,如果存在这样的划分,则称此图为二分图。 从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边······形成的路径叫交替路。 匈牙利



二分图最小覆盖数 最大匹配数与最大独立集 隙间



二分图 Mini Coconut 博客园
二分图的最大独立集 今天是开通博客的第一天 ,现在参加牛客暑假多校训练赛, 恰好在补网络流二分图的题,就顺便把比赛这道题搬出来了 提示(本题需要的前序知识 ,网络流算法 ,二分图匹配,最大匹配 ,最小边覆盖,最大独立集 ,最小点覆盖) · 二分图多重匹配 网络最大流 8 机器人路径规划问题 (未解决) 最小费用最大流 9 方格取数问题 二分图点权最大独立集 网络最小割 10 餐巾计划问题 线性规划网络优化 最小费用最大流 11 航空路线问题 最长不相交路径 最小费用最大流 12 软件补丁问题 最小转移代价 最短路径 13 星际转移问题 网络判定 网络最大流 14 孤岛营救问题 分层图最短路径 最短路径 15二分图的最小顶点覆盖 最大独立集 最大团 1852 − 二分图的最小顶点覆盖 定义:假如选了一个点就相当于覆盖了以它为端点的所有边。 最小顶点覆盖就是选择最少的点来覆盖所有的边。 方法:最小顶点覆盖等于二分图的最大匹配。 我们用二分图来




最大独立集算法的时间复杂度 Thinbug



网络流24题 23题分享 短暂出坑 代码天地
· 支配集、独立集、覆盖集 1 定义 11 支配集 设无向简单图 ,若 使得 ,则称 为 的一个支配集,并称 支配 。 设 是 的支配集,且 的任何真子集都不是支配集,则称 为极小支配集。 的顶点最少的支配集称作 的最小支配集。 最小支配集中的顶点个数称作 的支配数,记作 ,简记为 。 · 二分图(最大匹配,最小覆盖数,最大独立集合) 定义: 设G= (V, E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A , B),且图中的每条边(i, j)所关联的两个定点分别属于这两个不同的顶点集,则称图G为一个二分图。 性质: 定理:当且仅当无向图G的每一个环的结点数均是偶数时,图G才是一个二分图。 如果无环,相当于每的结点数为 0,故也视为二分图二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配




完全二分图 维基百科 自由的百科全书
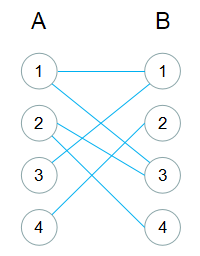
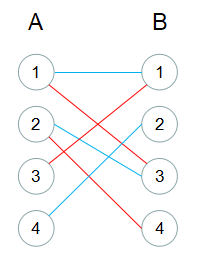
· 定理:二分图的最大团 = 补图的最大独立集 · 二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。 匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 · 二分图最大匹配 匈牙利算法 二分图的增广路:增广路是二分图中的一条路径。增广路的起点和终点都是未匹配点。增广路由已选择路径和未选择路径交替组成,也就是说,增广路含有的原本两部之间路径数量为奇数。




增广路径 程序员宅基地




顶点支配 独立与覆盖 华为云
· 一道基础的二分图最大独立集问题。 二分图的最大独立集 = n最小覆盖集 = n完美匹配数。 所以就转化成了二分图匹配,用匈牙利算法实现即可。 · 最大独立集问题 Given N sets of integers, remove some sets so that the remaining all sets are disjoint with one another Find the optimal solution so that the number of sets remaining at the end is maximum please explain your algorithm properly rather than pasting code最大流 (匈牙利算法)以及应用 分类: 匈牙利算法可以解决的图的问题:(二分图) 1图的最小点覆盖数 = 图的最大匹配数; 2图的最大点独立集 = 图顶点数 图的最大匹配数; 3图的最小路径覆盖数 = 原图的顶点数 原图拆点后形成的二部图



Oi之路 04图论 9二分图 Zory的个人博客
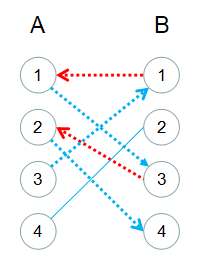



从二分图开始到最大匹配
· 最大独立集问题: 在N个点的图G中选出m个点,使这m个点两两之间没有边.求m最大值. 如果图G满足二分图条件,则可以用二分图匹配来做.最大独立集点数 = N 最大匹配数最大独立集 :顶点数最多的独立集。 顶点个数称为图G的独立数,记为α (G)。 如下图: 独立集: a,c, a,e, b,c, b,e, b,d, c,e, a,c,e, b,c,e 极大独立集: b,d,加入任何点都无法构成独立集;而 a,c不是极大独立集,还可以加入e构成更大的独立集 a,c,e 最大独立集: a,c,e, b,c,e二分图的最大独立集 二分图的最大独立集 194 0 0 作者摸鱼选手llf 今天是开通博客的第一天 ,现在参加牛客暑假多校训练赛, 恰好在补网络流二分图的题,就顺便把比赛这道题搬出来了



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




二分图最大匹配 简书
二分图(最小顶点覆盖 最大匹配 最大独立集 ) 1250 − 一、二分图的基本概念 二分图 二分图又称作二部图,是图论中的一种特殊模型。 设G= (V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集 (A,B),并且图中的每条边(i,j)所关联的/02/13 · 最大独立集: 独立集是指图的顶点集的一个子集,且该子集的导出子图不含边。 如果一个独立集不是任何一个独立集的子集, 那么称这个独立集是 一个极大独立集。一个图中包含顶点数目最多的独立集称为最大独立 v1v2 v3 v4 v5 v6 e1 e2 e3 e4 e5 例如对于图 21 来说二分图覆盖与独立集ppt 所需积分/C币: 6 1117 384KB PPTX 4 收藏 举报 版权声明 版权声明:该资源内容由用户上传,如若侵权请选择举报 网络流ppt,最小点覆盖,König定理:二分图中的最大匹配数=这个图中的最小点覆盖数,König定理证明,最小点覆盖
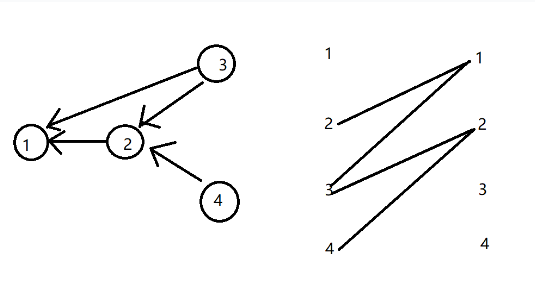



二分图最小覆盖数 最大匹配数与最大独立集 隙间
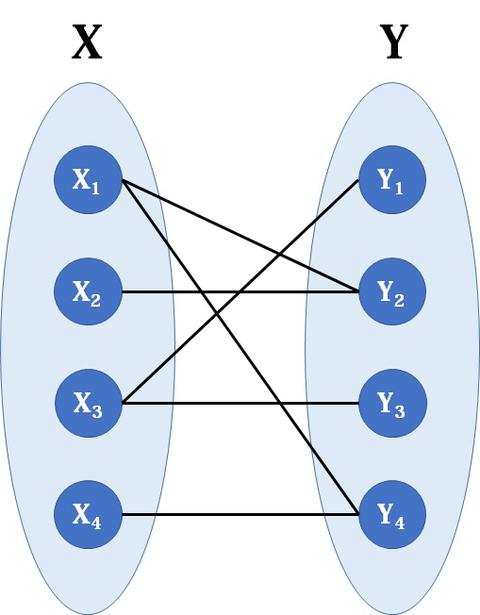



一中最菜菜鸡的博客 知乎
图匹配 匹配 或是 独立边集 是一张图中没有公共边的集合。 在二分图中求匹配等价于网路流问题。 图匹配算法是信息学竞赛中常用的算法,总体分为最大匹配以及最大权匹配,先从二分图开始介绍,在进一步提出一般图的作法。 · 可以证明:最少的点(即覆盖 数)=最大匹配数 最大独立集问题: (pku1466) 在N个点的图G中选出m个点,使这m个点两两之间没有 边.求m最大值. 如果图G满足二分图条件,则可以用二分图匹配来做.最大 独立集点数 = N 最大匹配数 相关题目 pku1325, pku1274 · 版权声明: 本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。 具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。 如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单



蒟蒻图论 二分图匹配 蒟蒻のblog




最小点覆盖 最大独立集 最少路径边覆盖 最少路径重复点覆盖 二分图小结 谁是凶手1703 Csdn博客
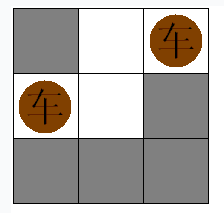
Stores the code of the problems I solved on HihoCoder faxinwang/HihoCoder · 建图方式类似于皇家卫士,也是利用行连通块和列连通块做点,单位泥地对应二分图中的边 要求放最少的板覆盖全部的泥地,转化为求最小覆盖 二分图最大独立集 图的独立集:寻找一个点集,其中任意两点在图中无对应边 二分图的最大独立集=图的点数最大匹配数二分图的最大独立集 黑色点即为一个最大独立集 简单解释 可以这样理解,在总的点集中,去掉最少的点,使得剩下的点相互之间没




二分圖最大獨立集 壹讀



Combinatorial Optimization Matroid Zhenweiliu S Blog



网络流模型总结 远航休息栈




二分图最大匹配 最大流 Thinkspiritlab
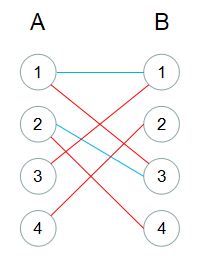



从二分图开始到最大匹配




二分图匹配问题 海边拾贝 沧海一粟 程序员宅基地 程序员宅基地



二分图最小覆盖数 最大匹配数与最大独立集 隙间
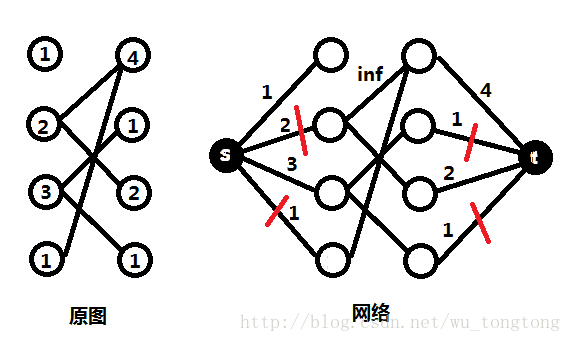



网络流专题2 二分图带权最大独立集 Picahor 博客园



Oi之路 04图论 9二分图 Zory的个人博客



算法设计与分析 0016 二分图匹配问题 Gary Chan S Blog




06 飞行员配对 二分图最大匹配 华为云
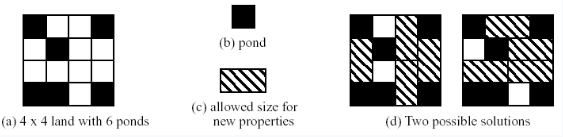



二分图最小覆盖数 最大匹配数与最大独立集 隙间
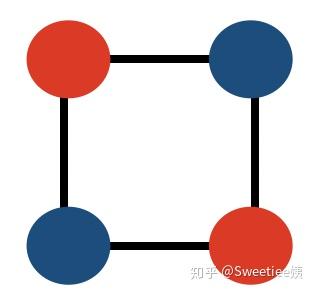



Leetcode每日打卡 判断二分图 知乎




二分图的最大匹配 最小顶点覆盖 最大独立集等价的线性规划证明 知乎
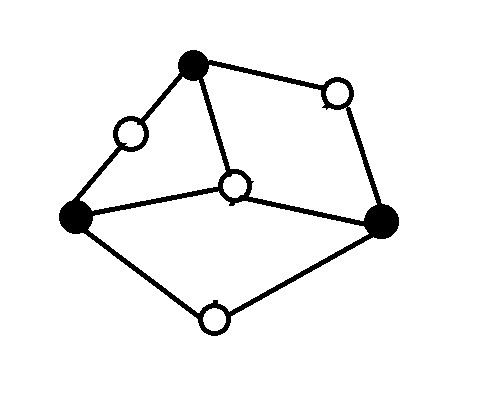



分布式算法3 最大独立集 Zakheav的专栏 Csdn博客




二分图 维基百科 自由的百科全书




最大独立集算法 21



蒟蒻图论 二分图匹配 蒟蒻のblog



二分图最小覆盖数 最大匹配数与最大独立集 隙间




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配




二分图最小覆盖数 最大匹配数 最大独立集 总数 最小覆盖集证明hdu 1068 Qzq Csdn博客




顶点支配 独立与覆盖 华为云



二分图的最大独立集 K码农




Hdu 39 二分图的最大独立集 牛客博客



图论2 江川 Ppt Download




Acm 程序设计计算机学院刘春英 1 Ppt Download



二分图的最大独立集 摸鱼选手llf 博客园



二分图最大匹配的konig定理及其证明 Matrix67 The Aha Moments



从二分图开始到最大匹配




二分图最小覆盖数 最大匹配数 最大独立集 总数 最小覆盖集证明hdu 1068 Qzq Csdn博客



Oi之路 04图论 9二分图 Zory的个人博客




二分图的最大匹配 最小顶点覆盖 最大独立集等价的线性规划证明 知乎



二分图染色与匈牙利 图论小知识 三 Acwing




二分图 搜索结果 哔哩哔哩 Bilibili




二分图 最大匹配 最小覆盖数 最大独立集合 牛客博客




二分图详解下载 Word模板 爱问共享资料




Ppt 二分图匹配powerpoint Presentation Free Download Id




二分图 牛客博客



二分图最小覆盖数 最大匹配数与最大独立集 隙间




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配



再谈二分图最大匹配 最小点覆盖 最小边覆盖与最大独立集 Icysky S Blog



二分图系列 二分图判定 匈牙利算法二分图的最大匹配 二分图最小点覆盖及最大独立集 Tham 博客园




Acm 程序设计计算机学院刘春英 1 Ppt Download




二分图题型总结与模板 Acwing




陈胤伯 浅谈图的匹配算法及其应用 阅读笔记 码农家园




二分图的最小顶点覆盖最大独立集最大团 朝拜明天 博客园



二分图染色与匈牙利 图论小知识 三 Acwing



从二分图开始到最大匹配




匈牙利算法 Issue 33 Nhjcacmt Acm Github




二分图最大匹配 最大流 Thinkspiritlab



Oi之路 04图论 9二分图 Zory的个人博客



蒟蒻图论 二分图匹配 蒟蒻のblog



Ppt 二分图匹配powerpoint Presentation Free Download Id



网络流模型总结 远航休息栈




Ppt 二分图匹配powerpoint Presentation Free Download Id



匹配算法 Daltao S Blog



二分图的最大独立集 Gvz S Blog



Poj 30 Antenna Placement 最大独立集 From A Start As An Acmer C 博客




今際の国の呵呵君 Algorithm Maximum Matching Of Bipartite Graph 二分图的最大匹配



二分图的最大匹配 最小顶点覆盖 最大独立集等价的线性规划证明 知乎



Oi之路 04图论 9二分图 Zory的个人博客



Oi之路 04图论 9二分图 Zory的个人博客




二分图中对最小顶点覆盖 最小边覆盖 最大独立集的理解 Iguodala的博客 Csdn博客 二分图最小边覆盖
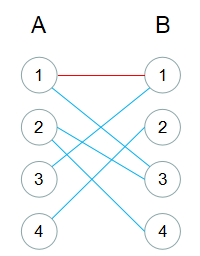



从二分图开始到最大匹配



蒟蒻图论 二分图匹配 蒟蒻のblog



蒟蒻图论 二分图匹配 蒟蒻のblog



Poj 3692 Kindergarten 题解 挑战程序设计竞赛 码农场




Acm 程序设计计算机学院刘春英 1 Ppt Download
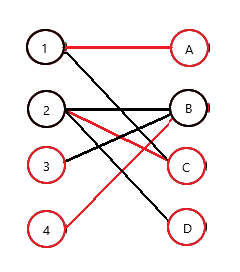



算法 二分图最大独立集 Skeletonking233的博客 Csdn博客




陈胤伯 浅谈图的匹配算法及其应用 阅读笔记 码农家园




Bapc 10 Gym j J Wrong Answer 二分图最大独立集 Ogmx的博客 Csdn博客
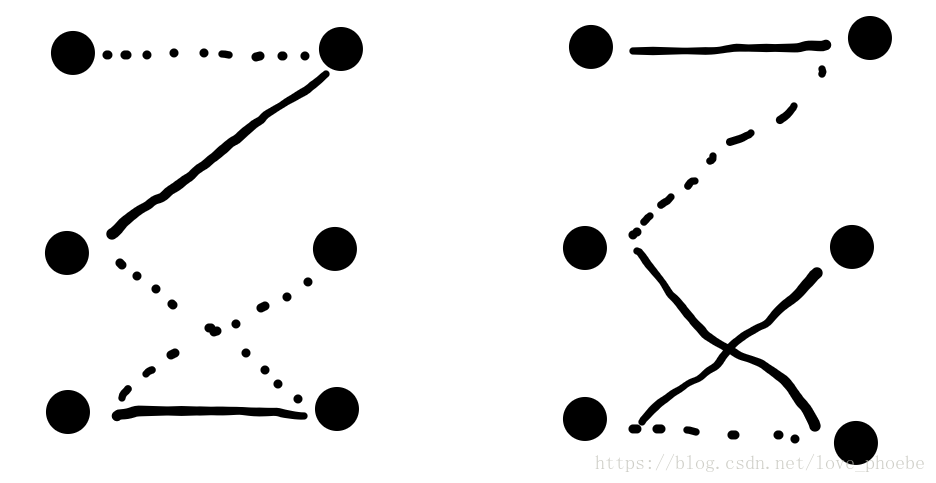



二分图匹配相关算法及例题分析最大匹配匈牙利算法最大权匹配km算法 二分图类型问题汇总 傻子是小傲娇的博客 大钊 程序员宅基地



蒟蒻图论 二分图匹配 蒟蒻のblog




Ppt 二分图匹配powerpoint Presentation Free Download Id
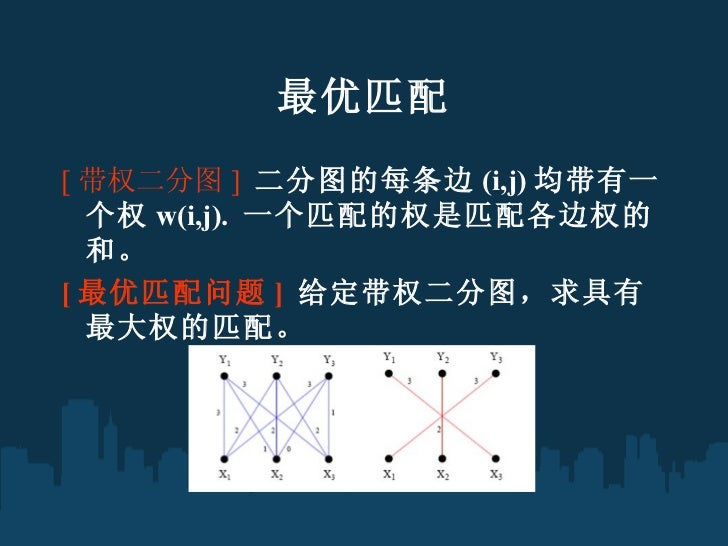



Acm图论



图论2 江川 Ppt Download
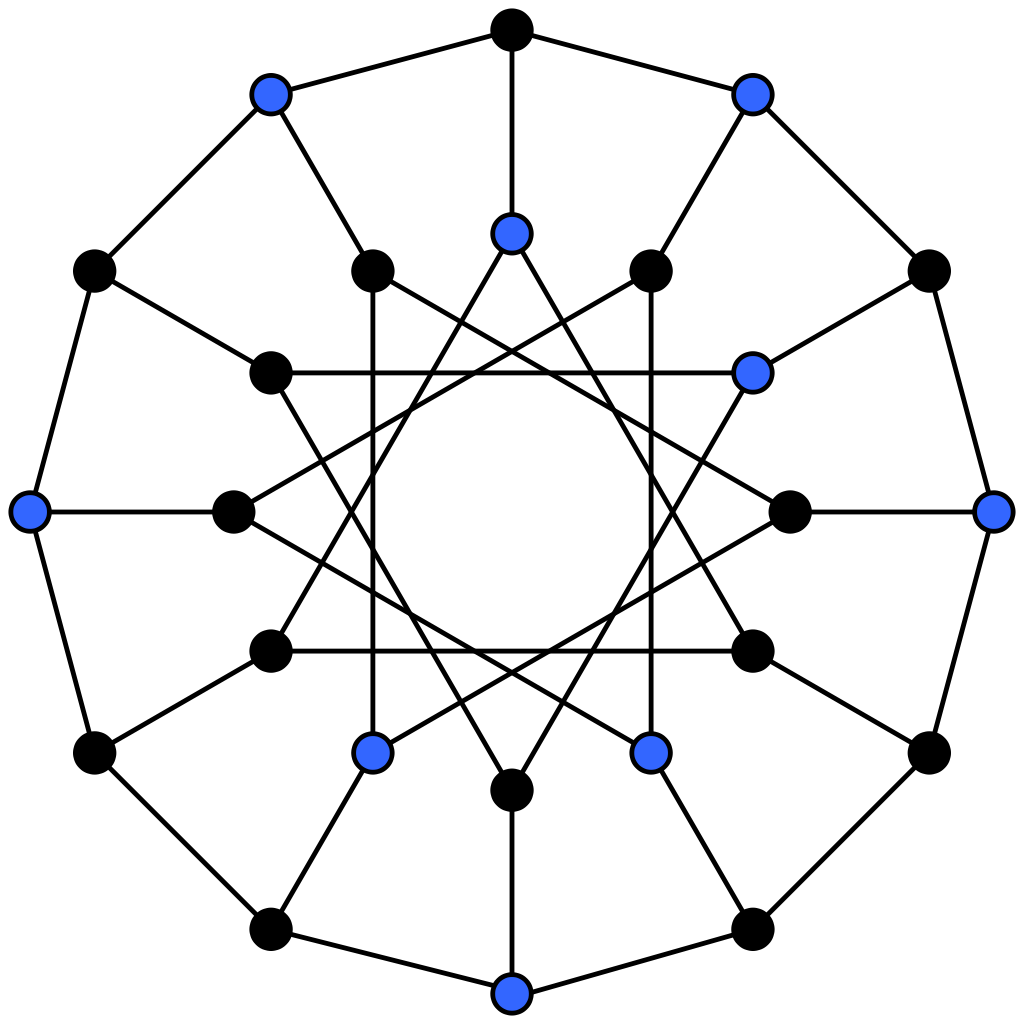



顶点独立集 知乎




二分图 网络流初步 Jzp 的博客 洛谷博客




Ppt 二分图匹配powerpoint Presentation Free Download Id




Bzoj 4808 马二分图最大独立集 Kaiser 博客园




二分图的最小顶点覆盖最大独立集最大团 朝拜明天 博客园




无向图的最大团 最大独立集 Osc T0xmr011的个人空间 Oschina 中文开源技术交流社区



0 件のコメント:
コメントを投稿